数学基础

1. 素数（质数）

定义：除了1和它本身以外不再有其它因素。

1.1 判断素数

枚举2~n,如果都除不尽，证明这个数是素数。时间复杂度O(n)。[+]

#include <iostream>
using namespace std;

bool isprime(int n){
	if(n<=3)
		return true;
	for(int i=2;i<n;i++){
		if(n%i==0)
			return false;
	}
	return true;
}

int main(){
	
	for(int i=1;i<=100;i++){
		printf("%3d is prime: %d \n",i,isprime(i));
	}
	
	return 0;
}

对于一个小于n的整数X，如果n不能整除X，则n必定不能整除n/X，所以只要从2枚举到

\sqrt{n}

即可。时间复杂度

O(\sqrt{n})

[+]

#include <iostream>
#include <cmath>
using namespace std;

bool isprime(int n){
	if(n<=3)
		return true;
	int rt = sqrt(n);
	for(int i=2;i<=rt;i++){
		if(n%i==0)
			return false;
	}
	return true;
}

int main(){
	
	for(int i=1;i<=100;i++){
		printf("%3d is prime: %d \n",i,isprime(i));
	}
	
	return 0;
}

根据对于大于等于1的自然x的来说，质数总等于6x-1或6x+1。
这是个必要条件，但不充分，也就是说等于6x-1或6x+1的数不一定是质数

也就是说等于6x-1或6x+1的数还要进一步判断是否为质数，即使这样也大大减少了判断数量[+]

#include <iostream>
#include <cmath>
using namespace std;

bool isprime(int n){
	if(n<=3)
		return true;
	if(n%6!=1 && n%6!=5)
		return false;
		
	int rt = sqrt(n);
	for(int i=5;i<=rt;i+=6){
		if(n%i==0 || n%(i+2)==0)
			return false;
	}
	return true;
}

int main(){
	
	for(int i=1;i<=100;i++){
		printf("%3d is prime: %d \n",i,isprime(i));
	}
	
	return 0;
}

证明一下：

首先6x肯定不是质数，因为它能被6整除；
其次6x+2肯定也不是质数，因为它还能被2整除；
依此类推，6x+3肯定能被3整除；6x+4肯定能被2整除；
那么，就只有6x+1和6x+5(即等同于6x-1)可能是质数了。

1.2 求1~n的所有素数

一般线性筛选法[+]

#include <iostream>
using namespace std;

const int maxn = 100000005;
int used[maxn],number[maxn];

int prime(int n){
	int cnt=0;
	for(int i=2;i<=n;i++){
		if(!used[i]){
			cnt++;
			number[cnt]=i;
		}
		for(int j=i*i;j<=n;j+=i){
			used[j]=true;
		}
	}
	return cnt;
}

int main(){
	
	int cnt = prime(100);
	
	for(int i=1;i<=cnt;i++)
		cout << number[i] << endl;
	
	return 0;
}

used

2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
-	-	1	-	1	-	1	2	1	-	1,2	-	1	2	1	-	1,2	-	1	2	1	-	1,2	3	1	2	1	-	1,2,3	-	1

number

1	2	3	4	5	6	7	8	9	10	11
2	3	5	7	11	13	17	19	23	29	31

这种方法比较好理解，初始时，假设全部都是素数，当找到一个素数时，显然这个素数乘上另外一个数之后都是合数。但仔细分析能发现，这种方法会造成重复筛除合数，影响效率。比如30，在i=2的时候，k=2*15筛了一次；在i=5，k=5*6的时候又筛了一次。所以，也就有了快速线性筛法。

快速线性筛选法[+]

#include <iostream>
using namespace std;

const int maxn = 100000005;
int used[maxn],number[maxn];

int prime(int n){
	int cnt=0;
	for(int i=2;i<=n;i++){
		if(!used[i]){
			cnt++;
			number[cnt]=i;
		}
		for(int j=1;(j<=cnt)&&(i*number[j]<=n);j++){
			used[i*number[j]]=true;
			if(i%number[j]==0)  //如i=6,则number[]={2,3,5},那么会用2*6消除12 
				break;			//但不会继续用3*6消除18，因为18会被i=9时消除 
		}
	}
	return cnt;
}

int main(){
	
	int cnt = prime(100);
	
	for(int i=1;i<=cnt;i++)
		cout << number[i] << endl;
	
	return 0;
}

used

2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
-	-	2	-	3	-	4	3	5	-	6	-	7	5	8	-	9	-	10	7	11	-	12	5	13	9	14	-	15	-	16

number

1	2	3	4	5	6	7	8	9	10	11
2	3	5	7	11	13	17	19	23	29	31

2. GCD与LCM

2.1 GCD：最大公约数

辗转相除法1（欧几里德法）[+]

int gcd1(int a,int b){
	if(a%b==0)
		return b;
	return gcd1(b,a%b);
}

[+]

int gcd2(int a,int b){
	int r=a%b;
	while(r){
		a=b;
		b=r;
		r=a%b;
	}
	return b;
}

穷举法[+]

int gcd3(int a, int b){
    int temp=(a>b)?b:a;
    while(temp>0){
        if(a%temp==0&&b%temp==0)
            break;
        temp--; 
    } 
    return temp;
}

更相减损法[+]

int gcd4(int m,int n){
    int i=0,temp,x=1;
    while(m%2==0&&n%2==0){
        m/=2;
        n/=2;
        i+=1;
	}
	if(m<n){
		temp = m;
		m=n;
		n = temp;
	}
    while(x){
    	x=m-n;
        m=(n>x)?n:x;
        n=(n<x)?n:x;
        if(n==(m-n)) break;
   	}
    if(i==0)
    	return n;
    else
		return (int) pow(2,i)*n;
}

Stein[+]

int gcd5(unsigned int x, unsigned int y){
    int factor = 0,temp;
    if(x < y){
    	temp = x;
        x = y;
        y = temp;
    }
    if ( 0 == y )
        return 0;
    while (x!=y){
    	if (x & 0x1 ){			/* when x is odd */
            if( y & 0x1 ){		/* when x and y are both odd */
            	y = (x - y) >> 1;
                x -= y;
            }else{				/* when x is odd and y is even */
                y >>= 1;
            }
        }else{					/* when x is even */
            if ( y & 0x1 ){		/* when x is even and y is odd */
                x >>= 1;
            	if ( x < y ){
                    temp = x;
                	x = y;
                	y = temp;
                }
            }else{				/* when x and y are both even */
                x >>= 1;
                y >>= 1;
                ++factor;
            }
    	}
    }
    return x << factor;
}

2.2 LCM：最小公倍数

[+]

int lcm1(int a,int b){
	int i;
	if(a<b)
		swap(a,b);
	for(i=a;;i++){
		if(i%a==0 &&i%b==0){
			break;
		}
	}
	return i;
}

2.3 GCD与LCM的关系

$gcd(a,b) \times lcm(a,b) = a \times b$
$lcm(a,b) = \frac{a \times b}{gcd(a,b)} = \frac{a}{gcd(a,b)} \times b$

[+]

int lcm2(int a,int b){
	return a / gcd(a,b) * b;
}

2.4 GCD与LCM满足分配率

gcd(a,lcm(b,c)) = lcm(gcd(a,b),gcd(a,c))
lcm(a,gcd(b,c)) = gcd(lcm(a,b),lcm(a,c))

2.5 例一：格点问题

在第一象限的格点(x，y), (x,y>=0)除原点外，能够被原点看到，当且仅当(x,y)与原点的连线不经过其他的格点。

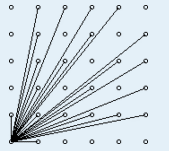
现给定正整数N，请计算纵坐标等于N的一行中有多少个(x,y)能够被原点看到。其中（0<=x<=N）

Sample Input

5
10

Sample Output

4
4

Sample Code

对于纵坐标N=10我们发现可以被看见的点是(1,10)、(3,10)、(7,10)、(9,10)其他点看不到的原因是，比如(4,10)点一定被(2,5)这一点遮挡。所以我们可以看得出我们需要求的就是gcd(i,N)==1的数。

注意： 在座标里，将点(0, 0)和(a, b)连起来，通过整数座标的点的数目（除了(0, 0)一点之外）就是gcd(a, b)。

[+]

#include <iostream>
using namespace std;

int gcd(int a,int b){
	int r = a%b;
	while(r){
		a = b;
		b = r;
		r = a % b;
	}
	return b;
}

int n,ans=0;

int main(){
	cin >> n;
	
	for(int i=1;i<=n;i++){
		if(gcd(i,n)==1){
			ans ++;
		}
	}
	
	cout << ans << endl;

	return 0;
}

2.6 例二：[NOIP2001普及组]最大公约数和最小公倍数问题

输入2个正整数x,y(2≤x≤100000，2≤y≤1000000)，求出满足下列条件的P、Q的个数。条件:

P、Q是正整数
要求P、Q以x为最大公约数，以y为最小公倍数。

试求，满足条件的所有可能的两个正整数的个数。

输入格式

2个正整数x,y

输出格式

1个数，表示求出满足条件的P,Q的个数

输入样例

3 60

输出样例

3,60
15,12
12,15
60,3

样例代码

我们知道P*Q/x=y,那么P*Q=x*y；
我们假设枚举P，那么Q=x*y/P,然后验证P、Q是否满足条件的要求，满足就是计数

[+]

#include <iostream>
using namespace std;

int x,y,p,q,ans=0;

int gcd(int a,int b){
	int r=a%b;
	while(r){
		a = b;
		b = r;
		r = a%b;
	}
	return b;
}

int lcm(int a,int b){
	return a / gcd(a,b) * b;
}

int main(){

	cin >> x >> y;
	
	for(p=1;p<=y;p++){
		q = y / p * x;
		if(gcd(p,q)==x && lcm(p,q)==y){
			ans ++;
		}
	}
	
	cout << ans << endl;
	
	return 0;
}

Exercise 1

蓄水池水管问题，http://noi.openjudge.cn/math/7648/[+]

#include <iostream>
using namespace std;

int main(){
	long long a,b,c,d;
	double t=0;
	
	cin >> a >> b >> c >> d;
	
	long long r= a*b*c*d;
	long long a2 = b*c*d;
	long long b2 = a*c*d;
	long long c2 = a*b*d;
	long long d2 = a*b*c;
	
	while(1){
		if(r>a2){
			r = r-a2;
			t = t +1;
		}else{
			t = t + (double)r/a2;
			break;
		}
		r = r + b2;
		t = t+1;
		if(r>c2){
			r = r-c2;
			t = t + 1;
		}else{
			t = t + (double)r/c2;
			break;
		}
		r = r + d2;
		t = t+1;
	}
	printf("%.2f",t);
	
	
	return 0;
}

我家的门牌号，http://noi.openjudge.cn/math/7649/[+]

#include <iostream>
using namespace std;

int main(){
	int n,flag = 0,home,my;
	
	cin >> n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			if((1+i)*i/2-2*j==n){
				home = i;
				my = j;
				flag = 1;
				break;
			}
		}
		if(flag)
			break;
	}
	cout << my << " " << home << endl;
		
	return 0;
}

自来水供给，http://noi.openjudge.cn/math/7651/[+]

#include <iostream>
using namespace std;
//                      ----
// a ======b ==== c ===d----e ----f---g
//                      ---   ----

const int maxn = ~((unsigned int)0)>>1;
const int N = 100;
int s[N+1],t[N+1];

int main(){
	
	int n,ans;
	cin >> n;

	s[0] = 0;
	t[0] = 0;
	for(int i=1;i<=n;i++){
		cin >> s[i];
		s[i] = s[i] + s[i-1]; 
		t[i] = t[i-1] + s[i];
	}		
	
	ans = maxn;
	for(int i=1;i<=n;i++)
		ans = min(ans,s[i]*8000+(t[n]-t[i]-(n-i)*s[i])*2000);
		
	cout << ans << endl;
		
	return 0;
}

乘积最大的拆分，http://noi.openjudge.cn/math/7652/[+]

#include <iostream>
using namespace std;

int n,ans[1005],p=0;

int main(){
	cin >> n;
	if(n==1){
		cout << 1 << endl;
		return 0;
	}
	for(int i=2;i<=n;i++){
		ans[p] = i;
		n = n - i;
		p++;
	}
	for(int i=p-1;i>=0 && n>0;i--){
		ans[i]++;
		n--;
	}
	if(n){
		ans[p-1]++;
	}
	for(int i=0;i<p;i++)
		cout << ans[i] << " ";
	cout << endl;
	
	return 0;
}

等差数列末项计算，http://noi.openjudge.cn/math/7654/[+]

#include <iostream>
using namespace std;
int a1,a2,n;

int main(){
	
	cin >> a1 >> a2 >> n;

	cout << a1+(n-1)*(a2-a1) << endl;

	return 0;
}

回文数个数，http://noi.openjudge.cn/math/7655/[+]

#include <iostream>
#include <cmath>
using namespace std;

int n,sum=0;

int main(){
	cin >> n;
	
	for(int i=1;i<=n;i++){
		int p = (i-1)/2;
		sum = sum + 9*pow(10,p);
	}

	cout << sum << endl;
	
	return 0;
}

李白的酒，http://noi.openjudge.cn/math/7656/[+]

#include <iostream>
using namespace std;

double d,h=1.0;
int n;

int main(){
	
	cin >> n;
	
	for(int i=n;i>=1;i--){
		h = h / 2 + 1.0;
	}
	
	printf("%.5lf\n",h-1);

	return 0;
}

连乘积末尾0的个数，http://noi.openjudge.cn/math/7657/[+]

#include <iostream>
using namespace std;

int a,b,ans2=0,ans5=0;

int count(int a,int mod){
	int cnt = 0;
	while(a%mod==0){
		cnt ++;
		a=a/mod;
	}
	return cnt;
}


int main(){
	cin >> a >> b;

	for(int i=a;i<=b;i++ ){
		ans2 = ans2 + count(i,2);
		ans5 = ans5 + count(i,5);
	}
	
	int ans = ans2<ans5?ans2:ans5;
	
	cout << ans << endl;
	
	return 0;
}

质数的和与积，http://noi.openjudge.cn/math/7827/[+]

#include <iostream>
#include <cmath>
using namespace std;

int s;
bool prime(int a){
	int r = sqrt(a);
	for(int i=2;i<=r;i++){
		if(a%i==0){
			return false;
		}
	}
	return true;
}

int main(){
	cin >> s;
	
	int t = s/2;
	
	for(int i=t;i<s;i++){
		if(prime(i) && prime(s-i)){
			cout << i * (s-i) << endl;
			break;
		}		
	}
	
	return 0;
}

最大公约数与最小公倍数，http://noi.openjudge.cn/math/7828/[+]

#include <iostream>
#include <cmath>
using namespace std;

int g,l,x,y;

int gcd(int n,int m){
	int r=n%m;
	while(r){
		r = n%m;
		n=m;
		m=r;
	}
	return n;
}

int main(){
	
	cin >> g >> l;
		
	int m=g*l;
	int r=sqrt(m);
	int ans = m;
	for(int i=1;i<=r;i++){
		if(m%i==0){
			x = i;
			y = m/i;
			int t = x + y;
			if(t<ans && gcd(x,y)==g)
				ans = t;
		}
	}	
	
	cout << ans << endl;
	
	return 0;
}

神奇序列求和，http://noi.openjudge.cn/math/7829/[+]

#include <iostream>
#include <list>
using namespace std;

int a[2][1000],n,x,y;

int main(){
	int len=2,src,dst,p,ans=0;

	cin >> x >> y >> n;

	a[0][0]=x;
	a[0][1]=y;	
	for(int i=0;i<n;i++){
		src = i%2;
		dst = (i+1)%2;
		p=0;
		for(int j=0;j<len-1;j++){
			a[dst][p++] = a[src][j];
			a[dst][p++] = a[src][j]+a[src][j+1];
		}
		a[dst][p++] = a[src][len-1];
		len = p;
	}	
	for(int j=0;j<len;j++)
		ans = ans + a[dst][j];
		
	cout << ans << endl;
	
	return 0;
}

最接近的分数，http://noi.openjudge.cn/math/7832/[+]

#include <iostream>
using namespace std;

int n,x,y;
double a,b,mx=-0.1;

int main(){
	cin >> n >> a >> b;
	
	double t = a/b;
	for( int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			double z = double(i)/double(j);
			if(z<t && z > mx ){
				mx = z;
				x = i;
				y = j;
			}	
		}
	}
		
	cout << x << " " << y << endl;
	
	return 0;
}

分成互质组，http://noi.openjudge.cn/math/7834/

[+]

#include <iostream>
using namespace std;

int n,f[1000],a[1000],v[1000],ans=0;

int gcd(int a,int b){
	int r = a % b;
	while(r){
		a = b;
		b = r;
		r = a % b;
	}
	return b;
}

int find(int x){
	if(f[x]!=x) f[x]=find(f[x]);
	return f[x];
}

bool check(int x,int y){
	int f = find(x);
	for(int i=1;i<=n;i++){
		if(find(i)==f && i!=y){
			if(gcd(a[i],a[y])!=1)
				return false;
		}
	}
	return true;
}

int main(){
	cin >> n;
	for(int i=1;i<=n;i++){
		cin >> a[i];
		f[i]=i;
	}
	v[1]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i!=j && v[j]!=1){
				if(check(i,j)){
					f[j]=find(i);
					v[j]=1;
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(f[i]==i)
			ans++;
	}
	cout << ans << endl;
	
	return 0;
}

[+]

#include <iostream>
#include <vector>
using namespace std;

vector< vector<int> > g;
int n,a[100];

int gcd(int x,int y){
	int r=x%y;
	while(r){
		x = y;
		y = r;
		r = x % y;
	}
	return y;
}

int main(){
	cin >> n;
	for(int i=1;i<=n;i++)
		cin >> a[i];
		
	vector<int > v;
	v.push_back(a[1]);
	g.push_back(v);
	
	for(int p=2;p<=n;p++){
		int flag1 = 1;
		for(int i=0;i<g.size();i++){
			int flag2 = 1;
			for(int j=0;j<g[i].size();j++){
				if(gcd(a[p],g[i][j])!=1){
					flag2 = 0;
					break;
				}
			}
			if(flag2){
				g[i].push_back(a[p]);
				flag1 = 0;
				break;
			}
		}
		if(flag1){
			vector<int> t;
			t.push_back(a[p]);
			g.push_back(t);
		}			
	}

	
	cout << g.size() << endl;
	
	return 0;
}